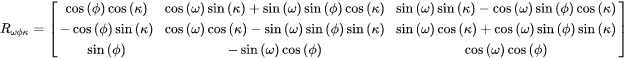Mathematical Equations Used with Boresighting

This section provides information regarding the equations used by the boresighting module. The photogrammetric equation is typically presented as Equation 1.

Equation 1

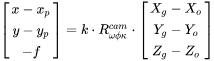
Where:	x,y	image coordinates
	xp, yp	principal point offset
	f	focal length
	k	scale factor
	Xg, Yg, Zg	ground coordinates
	Xo, Yo, Zo	perspective center coordinates

The boresighting feature solves for a rotation required in the derivation of the matrix, which represents the attitude of the image coordinate system with respect to the ground coordinate system. This matrix is defined through Equation 2.

Equation 2

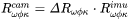
Inertial Explorer’s boresighting module provides the rotation angles that form the ΔR_wok matrix. The other rotation matrix, , is computed from Equation 3. In this equation, R_c accounts for the different axes definition between the camera and the IMU.

Equation 3

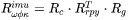
In general, when a conventional image frame is employed, the R_c is computed by Equation 4.

Equation 4

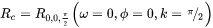
The quantity R_g corrects for the map convergence and is computed by Equation 5.

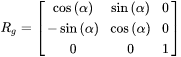
Where:

α

is the difference between grid north and true north

The final quantity required to solve for is R_rpy, which represents the rotation required to orientate the IMU into the ground coordinate system and is computed by Equation 6.

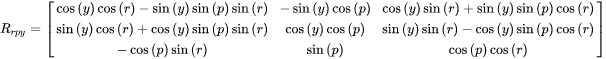
Where:	r	roll angle
	p	pitch angle
	y	yaw angle

yaw = –heading

It is also useful to present the matrix required to rotate a ground coordinate system into an alternate coordinate system. This matrix is defined through Equation 7.